Funções de uma variável

Semana 1

Taxa de variação

Suponha que $y = f(x)$ seja uma função de $x$. Se $x$ variar entre dois pontos $x_1$ e $x_2$, então a variação de $x$ será $\Delta x = x_2-x_1$ e a variação correspondente de $y$, $\Delta y = f(x_2)-f(x_1) = y_2-y_1$. O quociente dessas diferenças, ou seja,

é denominado taxa de variação média de $y$ em relação a $x$. Fazendo $x_2$ tender a $x_1$, de modo que $\Delta x \rightarrow 0$ , o limite de taxa média de variação é denominado taxa de variação instantânea de $y$ em $x = x_1$ e é dado por

Observe que, no cálculo da taxa de variação instantânea em $x_1$, o ponto $x_2$ é um ponto arbitrário e pode ser substituído por $x$ . Neste caso teremos,

Exemplo

Dada a função $f(x)=4x^3$, iremos calcular as taxas de variação média e instantânea em torno de $x_1=2$. A taxa de variação média será dada por

Tomemos alguns pontos $x_2$ maiores e menores do que $x_1$ e vejamos como eles se comportam. Isso é dado na tabela abaixo:

A tabela acima sugere que a variação instantânea de $f(x)$ está entre 50,44 e 45,64. Vejamos se de fato é o caso.

Portanto a taxa de variação instantânea está no intervalo sugerido pela tabela. Mas cuidado, resultados como o da tabela acima podem nos levar a conclusões errôneas. O limite te dará o resultado correto.

Exercício

Seja $y = x^2$. Calcule a taxa média de variação de $y$ em relação a $x$ com $x_1=1$ e $x_2=\frac{1}{{2}},\, \frac{1}{10}$ e $\frac{1}{10^{10}}.$ Calcule também a taxa de variação instantânea em $x_1 =1$.

Reta tangente

A palavra tangente vem do latim tangens, que significa “tocando”. Assim, uma tangente a uma curva é uma reta que toca a curva. Em outros termos, uma reta tangente deve ter a mesma direção que a curva no ponto de contato. Como tornar precisa essa ideia?

Exemplo

Encontre uma equação da reta tangente à parábola $y =x^2$ no ponto $P=(1, 1)$ .

Solução

Podemos encontrar uma equação da reta tangente t assim que soubermos sua inclinação $m$. A dificuldade está no fato de conhecermos somente o ponto $P$, quando precisamos de dois pontos para calcular a inclinação (dada pela taxa variação média). Observe, porém, que podemos calcular uma aproximação da inclinação $m$ escolhendo um ponto $Q=(x, x^2)$ sobre a parábola, próximo a $P$. Com isso calculamos a inclinação $m_{PQ}$ da reta secante $PQ$ ¹. Escolhemos $x \approx 1$² de forma que $Q \approx P$ . Com isso obtemos a inclinação

A animação abaixo mostra a reta tangente a $y=x^2$ no ponto $(1,1)$ e retas secantes com diferentes inclinações.

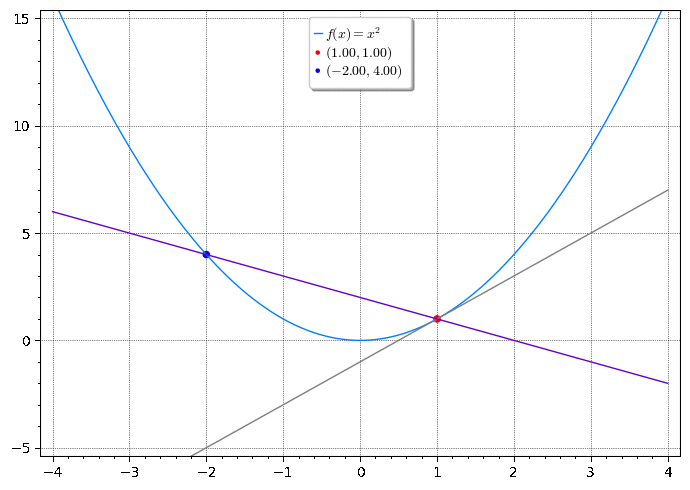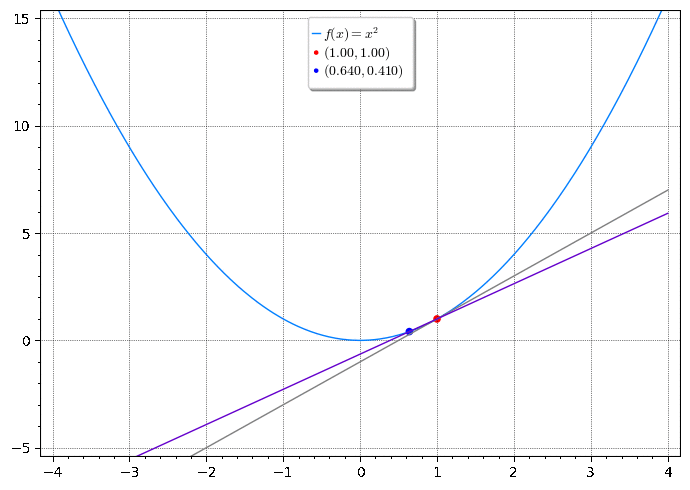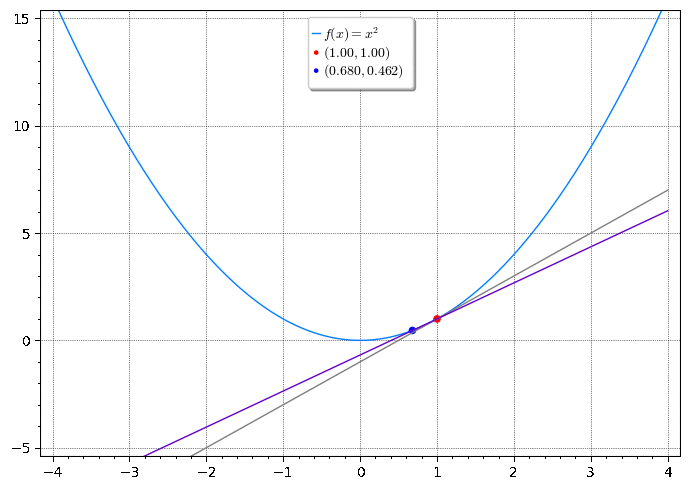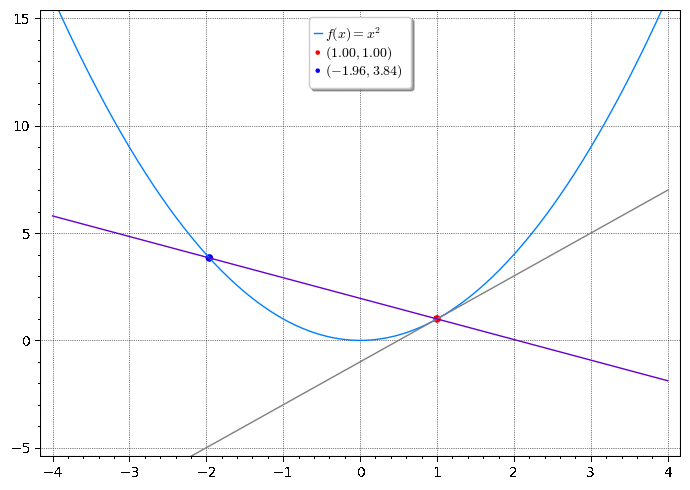
A tabela abaixo mostra os valores de $m_{PQ}$ para vários valores de $x$ próximos a 1. Quanto mais próximo $Q$ estiver de $P$, mais próximo $x$ estará de 1, e a tabela indica que $m_{PQ}$ estará mais próximo de 2.

A tabela acima sugere que a inclinação da reta tangente é o limite das inclinações das retas secantes, como de fato estabelece a definição a seguir.

Definição

A reta tangente a uma curva $y= f(x)$ em um ponto $P=(a, f(a))$ é a reta que passa por $P$ e que tem a inclinação dada por

$$m=\lim_{x\rightarrow a}\frac{f(x)-f(a)}{x-a},$$

desde que esse limite exista.

Então, para encontrar a reta tangente a uma curva $y= f(x)$ em um ponto $P=(a, f(a))$, primeiro calculamos a inclinação $m$ da reta tangente conforme a definição, e em seguida, usamos a equação da reta,

No ponto $P=(a, f(a))$ isso resulta em

A animação abaixo mostra o a reta tangente à $f(x)=x^4-5x^2+4$ em diferentes pontos.

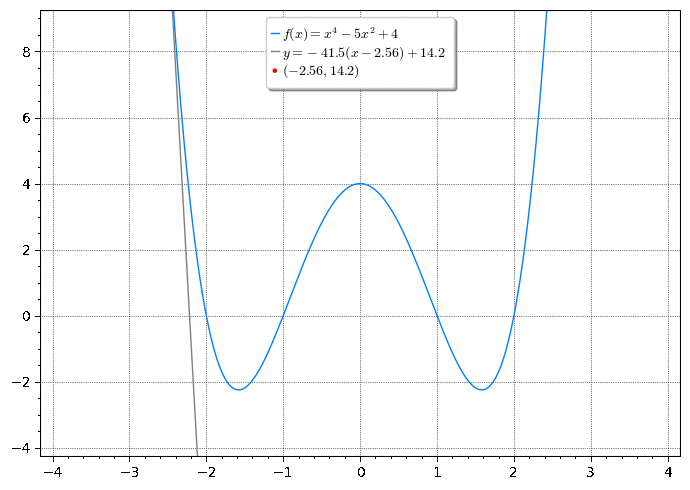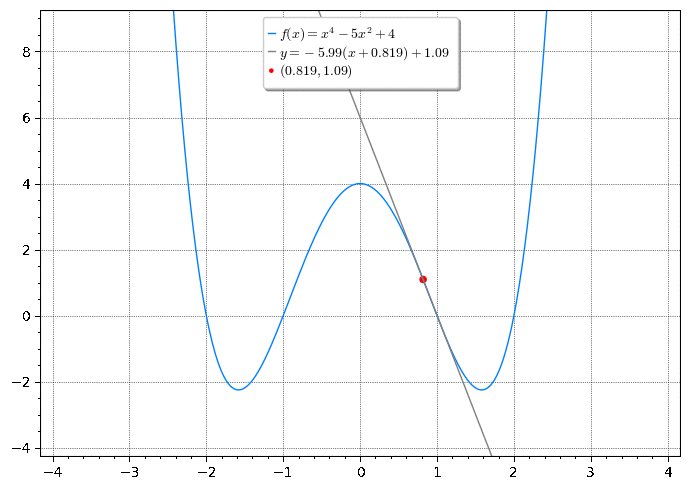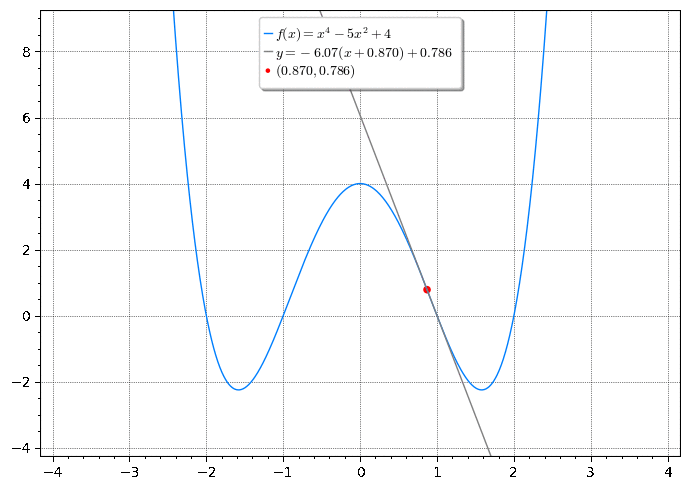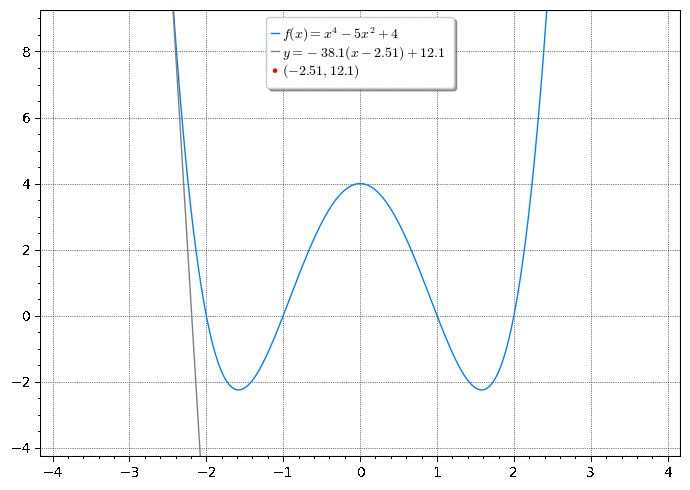
Exercício

Encontre a equação da reta tangente à curva no ponto dado.

1. $y= x^2,\ P=(1,\ 1).$
2. $y = \sqrt{2x+1},\ P =(4,\ 3).$
3. $y =x^3,\, P=(1,1).$

Observe que a inclinação da reta tangente a $y= f(x)$ em um ponto $P=(a, f(a))$ pode ser calculado através de

Basta considerar $h = x-a$ na definição. Retornaremos a discutir sobre essa forma de representar a inclinação da reta tangente.

Velocidade

Suponha que um objeto esteja se movendo sobre uma linha reta de acordo com a equação $s = f(t)$, onde $s$ é o deslocamento do objeto a partir da origem no instante $t$. A função $f(t)$ é chamada função posição do objeto. A velocidade média do objeto no intervalo $[a, a+h]$ é

Já a velocidade instantânea, ou simplesmente a velocidade, do objeto no instante $t=a$ é

Exemplo

Considere um objeto se movendo com função posição dada por $s(t) = 4,9t^2$. Determine a velocidade instantânea desse objeto no instante $t=a$.

Solução

Encontrar a velocidade instantânea em $t=a$ equivale a calcular a inclinação da reta tangente nesse ponto, como ilustrado no figura abaixo

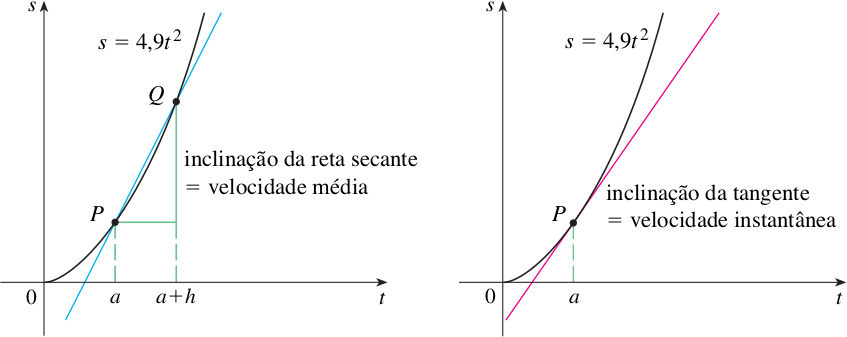
Logo,

Exercício

Considere uma bola atirada ao ar com uma velocidade de 40 pés/s. Sua altura (em pés) depois de $t$ segundos é dada por $y = 40t-16t^2$. Encontre a velocidade quando $t=2$.

Derivadas

Vimos que a inclinação da reta tangente à curva $y= f(x)$, a velocidade de um objeto com função posição $s= f(t)$ no instante $t =a$, e de forma mais geral, a taxa instantânea de variação de $y$ em relação a $x$ no ponto $x=a$, são todas calculadas da mesma maneira. Ambos os casos são determinados a partir do limite

Uma vez que esse tipo de limite ocorre com bastante frequência, ele recebe um nome e uma notação especial, conforme definição a seguir.

Definição

A derivada de uma função $f$ em um ponto $x_0 = a$, denotada por $f'(a)$, é

$$f'(a) = \lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}$$

se o limite existe.

Observe que a derivada de $f(x)$ em $x=a$ pode ser calculado através de

Basta considerar, como anteriormente, $x = a+h$ na definição acima.

Portanto, de acordo com as definições anteriores, a inclinação da reta tangente, velocidade instantânea e taxa instantânea de variação são todas dadas pela derivada de uma função $y = f(x)$.

A estratégia geral para se calcular uma derivada a partir da definição é manipular o limite de modo a remover a indeterminação, geralmente eliminando potencias de $h$ no numerador com o $h$ do denominador.

Geralmente dizemos derivar uma função como sinônimo de calcular a derivada de uma função.

Exercício

Seja $f(x) = x^2-x+1$. Encontre $f'(1)$ e use-a para determinar a equação da reta tangente à curva $f(x)$ no ponto $(1,f(1))=(1,\ 1)$.

A derivada como uma função

Até agora aprendemos como calcular a derivada de uma função em um ponto dado. Agora, vamos supor que esse ponto possa variar. Então, substituindo $a$ por $x$ na definição de derivada, temos

Neste caso, a função $f'(x)$ é dita derivada de $f$. Consequentemente $f'(x)$ pode ser interpretado geometricamente como a inclinação da reta tangente ao gráfico de $f$ no ponto $(x,f(x))$.

Exemplo

Um fabricante produz peças tecido com largura fixa. O custo de produção de $x$ metros de certo tecido, em reais, é dado por $C(x)$.

(a) Qual o significado da derivada $C'(x)$? Quais são suas unidades?

(b) Em termos práticos, o que significa dizer que $C'(1000)=9$?

Solução

(a) A derivada $C'(x)$ é a taxa de variação instantânea de $C(x)$ em relação a $x$. Isto é, $C'(x)$ representa a taxa de variação do custo de produção em relação à quantidade de metros produzidos (os economistas chamam essa taxa de variação de custo marginal). Se $C'(a)>0$, então produzir mais do que $a$ metros implica em aumento do custo de produção por metro. Por outro lado, $C'(a)<0$ implica em redução do custo de produção por metro. Como

as unidades de $C'(x)$ são iguais às do quociente de diferenças $\frac{\Delta C}{\Delta x}$ . Uma vez que $C(x)$ é medida em reais e $x$ em metros, segue que a unidade para $C'(x)$ é reais por metro.

(b) A afirmação que $C'(1000)=9$ significa que, depois de 1 000 metros da peça terem sido fabricados, a taxa segundo a qual o custo de produção está aumentando é R$ 9/m (quando $x = 1 000$, $C$ está aumentando 9 vezes mais rápido que $x$).

Gráfico de $f(x)$ $\times$ Gráfico de $f'(x)$

Como $f'(x)$ representa, a cada ponto, a inclinação da reta tangente a $f(x)$, os gráficos de $f(x)$ e de $f'(x)$ estão intimamente relacionados. Nos intervalos onde $f(x)$ é crescente, $f'(x)$ será positiva, onde $f(x)$ é descrescente, $f'(x)$ será negativa. Preste atenção neste comportamento na animação abaixo.

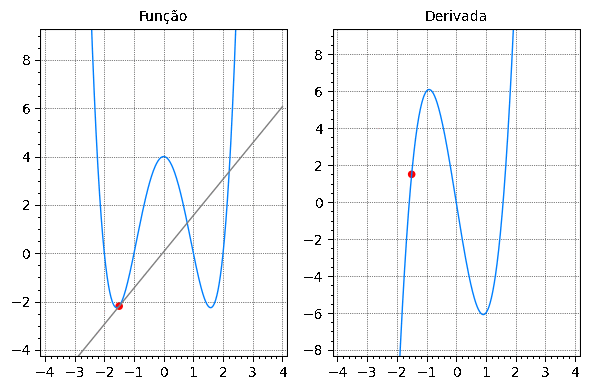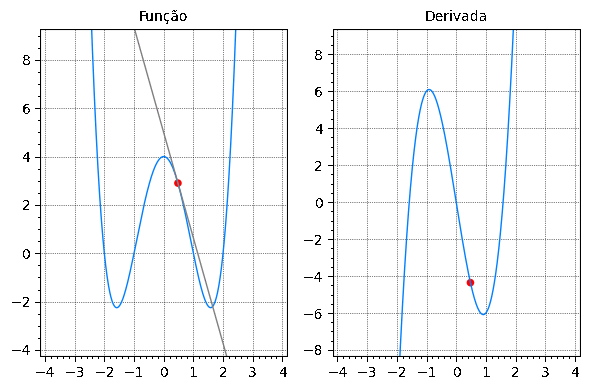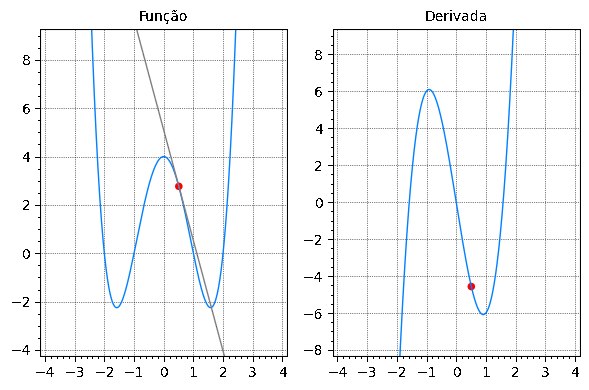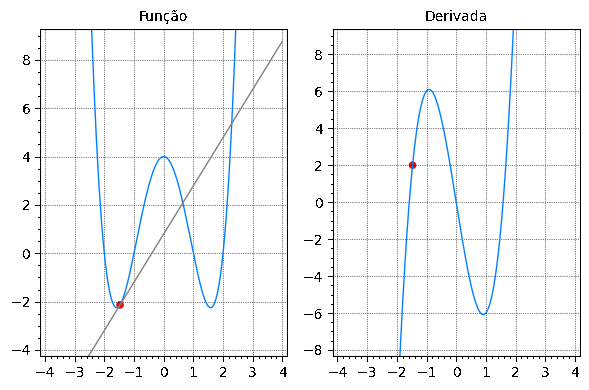
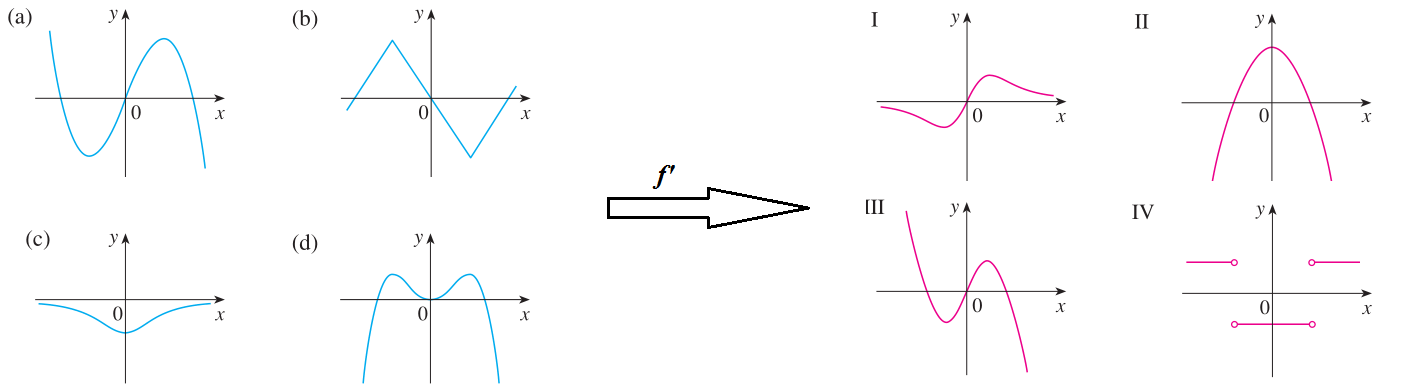
Exercício

Associe o gráfico de cada função em (a)-(d) com o gráfico de sua derivada em I-IV na figura dada abaixo. Justifique sua escolhas.

Funções diferenciáveis

Definição

Uma função $f$ é diferenciável em $a$ se $f'(a)$ existir. É diferenciável em um intervalo aberto $(a,b)$ [ou $(a,\infty)$ ou $(-\infty, a)$ ou $(-\infty, \infty)$] se for diferenciável em cada número do intervalo.

Como é uma função não diferenciável?

Em geral, se o gráfico de uma função $f(x)$ tiver uma “quina” ou uma “dobra”, então o gráfico de $f(x)$ não terá tangente nesse ponto e $f(x)$ não será diferenciável ali. (Ao tentar calcular $f'(a)$ , vamos descobrir que os limites à esquerda e à direita são diferentes). Uma outra forma de uma função deixar de ter uma derivada é se ela não for contínua, conforme estabelece o teorema abaixo. Uma terceira possibilidade surge quando a curva tem uma reta tangente vertical quando $x =a$; isto significa que $\lim_{x\to a}|f'(x)|=\infty$.

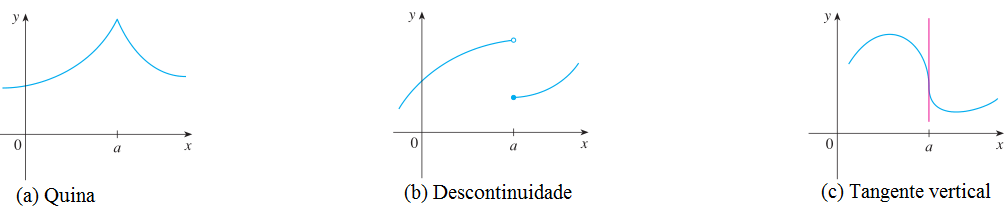
Exercício

A função $f(x)=|x|$ é diferenciável na origem? Verifique se o limite dado na definição de derivada existe nesse ponto.

Tanto a continuidade como a diferenciabilidade são propriedades desejáveis em uma função, principalmente nas diversas aplicações do cálculo. O seguinte teorema mostra como essas propriedades estão relacionadas.

Teorema

Se $f$ for diferenciável em $a$, então $f$ é contínua em $a$.

Demonstração

Para demonstrar que $f$ é contínua em $a$, temos de mostrar que $\lim_{x\to a}f(x)=f(a)$. Ou equivalentemente, $\lim_{x\to a}\left[f(x)-f(a)\right]=0$. Logo,

Na primeira linha da demonstração simplesmente multiplicamos e dividimos por $x-a$. Na segunda usando uma propriedade de limites e na terceira usamos a definição de derivada. Com isso $\lim_{x\to a}\left[f(x)-f(a)\right]=0$ e o teorema está demonstrado.

Responda: se $f$ for contínua em $a$, então $f$ é necessariamente diferenciável em $a$?

Outras notações Podemos usar cada uma das seguintes notações para representar as derivadas:

Derivadas de funções polinomiais

Antes de qualquer coisa lembremos que uma função polinomial de grau $n$ é uma função do tipo

com $a_0,a_1,\ldots,a_n$ constantes.

Ok, mas agora como calculamos a derivada de uma função polinomial? Vamos começar com casos simples. Primeiramente, calcule $\frac{d}{dx}c$, onde $c$ é uma constante, usando a definição de derivada.

Nos exemplos, já calculamos $\frac{d}{dx}x^2$ e $\frac{d}{dx}x^3$. Note que há um padrão aqui, $\frac{d}{dx}x^2 = 2x$ e $\frac{d}{dx}x^3 = 3x^2$. No caso geral, $\frac{d}{dx}x^n$, onde $n$ é um inteiro positivo, será dada por

Logo, dado o polinômio $p(x) = a_0+a_1x+a_2x^2+\cdots +a_nx^n,$ temos

Demostração

Primeiramente vamos provar o caso $p(x) = x^n$ usando o teorema binomial, o caso de um polinômio geral será consequência da propriedade de linearidade da derivada, que será discutido na próxima seção.

Sabemos que

Mas como calculamos, por exemplo, $\frac{d}{dx}\sqrt{x}=\frac{d}{dx}x^{1/2} = \frac12x^{-1/2}$?

A regra de derivação de polinômios se estende ao caso mais geral onde $n$ é um número real qualquer, de modo que

Demonstraremos esse resultado quando discutirmos sobre derivadas de funções logarítmicas.

Linearidade da derivada

Quando novas funções são formadas a partir de outras por adição, subtração, multiplicação ou divisão, suas derivadas podem ser calculadas em termos das derivadas das funções originais. Suponha que $f$ e $g$ sejam funções diferenciáveis e $c$ uma constante. Então:

1. $\frac{d}{dx}[cf(x)]=c\frac{d}{dx}f(x)=c f'(x);$
2. $\frac{d}{dx}[f(x)+g(x)]=\frac{d}{dx}f(x)+\frac{d}{dx}g(x)=f'(x)+g'(x);$
3. $\frac{d}{dx}[f(x)-g(x)]=\frac{d}{dx}f(x)-\frac{d}{dx}g(x)=f'(x)-g'(x).$

Exercício

Use a definição de derivada para demostrar as propriedades 1,2 e 3 acima.

Essas propriedades, que decorrem da definição de derivada, podem ser representadas de forma mais sucinta por

Exercícios

Calcule as derivadas das seguintes funções:

$$\begin{aligned} 1.\; & f(x) = x^2+3x-4,\\ 2.\; & f(x) =(2x^3+3)(x^4-2x). \end{aligned}$$

Derivadas de funções exponenciais

Lembrando que uma função exponencial é uma função do tipo $f(x) = a^x$, onde $a>0$ e $a\neq 1$.

Usando a definição de derivada, vamos agora provar que se ${f(x) = a^x}$, então

De fato,

Observe que $f'(0) =\lim\limits_{h\rightarrow 0}\frac{a^h-1}{h}$.

A equação $f'(x) = f'(0)a^x$ nos diz que a taxa de variação de qualquer função exponencial é proporcional à própria função (a inclinação é proporcional à altura).

De todas as possíveis escolhas para a base $a$ vamos agora nos ater ao caso mais simples e importante, o caso em que $f' (0) = 1$. Essa base, denotada por $e$ e denominada número de Euler, é definida a seguir

Definição

$e$ é um número real tal que $\lim\limits_{h\rightarrow 0}\frac{e^h-1}{h}=1.$

Geometricamente, isso significa que, de todas as possíveis funções exponenciais $y = a^x$ , a função $f(x)=e^x$ é aquela cuja reta tangente em ( 0, 1) tem uma inclinação $f'(0)$, que é exatamente 1.

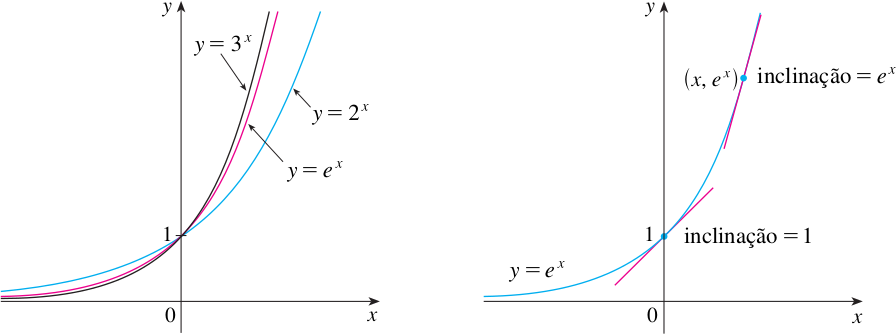
Se pusermos $a = e$ , e consequentemente, $f'(0)= 1$ na derivada de $a^x$, teremos a seguinte importante fórmula de derivação:

Derivada da função exponencial natural

Isso estabelece a derivada de funções exponenciais de base $e$. Retornaremos ao caso geral quando discutirmos sobre derivadas de funções logarítmicas.

Exercícios

1. Em que ponto da curva $y = e^x$ sua reta tangente é paralela à reta $y = 2x$?
2. Para quais valores de $a$ e $b$ a reta $2x + y = b$ é tangente à parábola $y = ax^2$ quando $x = 2$?

Regra do produto e regra do quociente

As fórmulas que introduziremos agora, que também decorrem da definição de derivada, nos permitem derivar novas funções formadas a partir de funções conhecidas por multiplicação ou divisão. Elas são conhecidas como regra do produto e regra do quociente.

Regra do produto

Se $f$ e $g$ são ambas deriváveis, então

Em outras palavras, a regra do produto diz que a derivada de um produto de duas funções é igual a primeira função vezes a derivada da segunda função mais a segunda função vezes a derivada da primeira função.

Demonstração da regra do produto

Exemplo

Se $f(x)=xe^x$ , encontre $f'(x)$.

Pela regra do produto,

Regra do quociente

Se $f$ e $g$ são ambas deriváveis, então

Exemplo

Derive a função $f(x) = \frac{x^2+x-2}{x^3+6}$.

Erros comuns: Cuidado, as expressões $(f(x)g(x))' = f'(x)g'(x)$ e $\left(\frac{f(x)}{g(x)}\right)' = \frac{f'(x)}{g'(x)}$ são incorretas.

Exercícios

1. Use a regra do quociente para mostrar que

   $$\frac{d}{dx}\left[\frac{1}{g(x)}\right]=-\frac{g'(x)}{g(x)^2}.$$

2. Use o resultado o exercício anterior para provar que a regra de potência é válida para inteiros negativos. Isto é,

   $$\frac{d}{dx}(x^{-n}) = -nx^{-n-1}.$$

3. Tente demonstrar a regra do quociente usando a definição de derivada.