Funções de uma variável

Semana 11

Comprimento do Arco

Gostaríamos de estabelecer, usando as técnicas que vimos até agora, uma forma de medir o comprimento de uma curva. Como poderíamos fazer isso? A pricípio, poderíamos pensar em usar um pedaço de barbante sobre a curva e então medir o comprimento do barbante. Mas além de pouco preciso, isso não é nada prático. Especialmente se estivermos lidando com uma curva complicada. Veremos agora uma forma de definir o comprimento de arco de uma curva de maneira precisa.

Se a curva é uma poligonal, podemos facilmente encontrar seu comprimento; apenas somamos os comprimentos dos segmentos de reta que formam a poligonal. Seguindo esta ideia, iremos definir o comprimento de uma curva geral primeiro aproximando-a por uma poligonal e, então, tomando o limite quando o número de segmentos da poligonal aumenta.

Dada uma curva $C$ definida pela equação $y = f(x)$ (onde $f$ é continua no intervalo $[a, b]$ e diferenciável no intervalo $(a,b)$), dividimos o intervalo $[a, b]$ em $n$ subintervalos com extremos $x_{0}=a, x_{1}, \ldots, x_{n}=b$ e com larguras iguais a $\displaystyle \Delta x = \frac{b-a}{n}$. Desta forma, se $y_i=f(x_i)$ então o ponto $P_i=(x_i,y_i)$ está na curva $C$ e a poligonal com vértices $P_0, P_1, \ldots, P_n$ (ilustrada na figura abaixo) é uma aproximação para $C$.

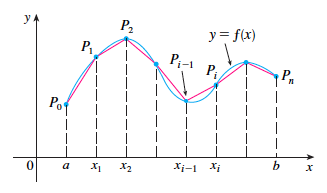
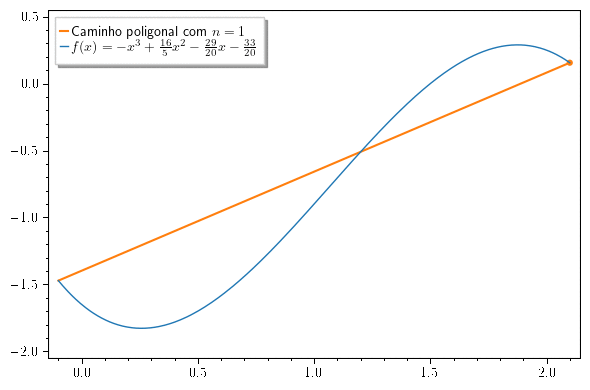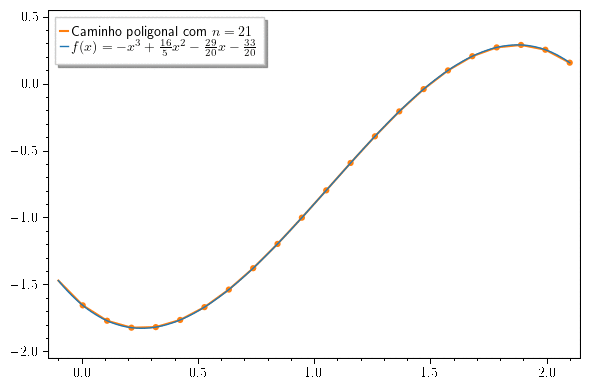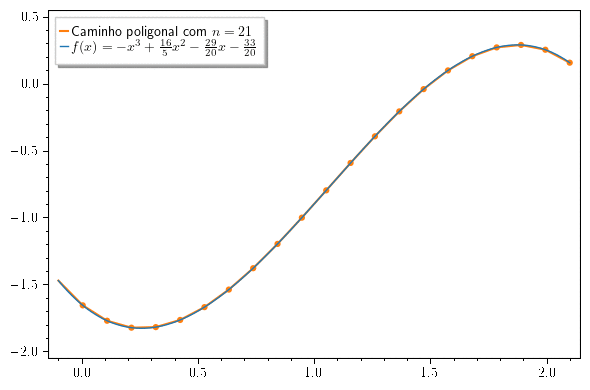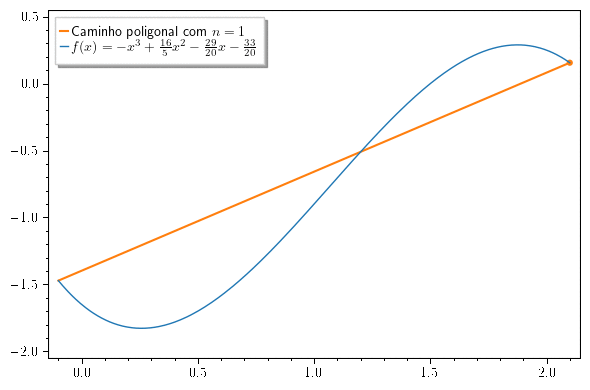
A aproximação do comprimento da curva $C$ pela poligonal fica cada vez melhor a medida que $n$ aumenta (veja a animação abaixo).

Definição

O comprimento L da curva C com equação $y=f(x)$, $a\leq x\leq b$, é o limite da soma dos comprimentos das poligonais que aproximam $C$, de modo que:

$$\begin{aligned} \nonumber \displaystyle L = \lim_{n\to \infty}\sum_{i=1}^n|P_{i-1}P_i|. \end{aligned}$$

Se o limite existir.

Reescrevendo a expressão acima obtemos

A definição de comprimento de arco que acabamos de ver não é muito conveniente para propósitos computacionais, mas podemos deduzir uma fórmula envolvendo uma integral para encontrar $L$, no caso em que $f$ tem uma derivada contínua. [Essa função $f$ é chamada lisa, porque uma pequena mudança em $x$ produz uma pequena mudança em $f^{\prime}(x)$.] Se tomarmos $\Delta y=y_i -y_{i-1}$, então usando o Teorema do valor Médio (Seção 2.2 das notas da semana 4) no intervalo $[x_i,x_{i-1}]$, sabemos que existe $x_i^\star\in (x_{i-1}, x_i)$, tal que

Desta forma,

Emfim, podemos enunciar o seguinte resultado:

Proposição: Fórmula do comprimento de arco

Se $f'$ for uma função contínua em $[a, b]$, então o comprimento da curva $y = f(x), a\leq x\leq b,$ é dado por

$$\boxed{L = \int_a^b\sqrt{1+(f'(x))^2}\,d x = \int_a^b\sqrt{1+\left(\frac{dy}{dx}\right)^2}\,dx}.$$

Observemos que se a função é dada como $x=f(y)$, $c\leq y\leq d$, basta trocar $x$ e $y$ na fórmula acima. Ou seja:

Exemplo

Calcule o comprimento de arco da curva dada.

1. $\displaystyle y = \ln(\cos(x)), 0\leq x\leq \pi/3$.
2. $\displaystyle x = \frac{y^3}3 + \frac{1}{4y}, \ 1\leq y\leq 2$.

Soluções:

1. Como $y = \ln(\cos(x))$, então $y' = -\tan(x)$. Assim,

Então

2. Como $\displaystyle x = \frac{y^3}3 + \frac{1}{4y}$, então $\displaystyle x' = y^2- \frac{1}{4y^2}$ e $\displaystyle 1+(x')^2 = 1+\left( y^2- \frac{1}{4y^2}\right)^2.$ Contudo,

   $$\begin{align*} 1+\left( y^2- \frac{1}{4y^2}\right)^2&={4} + \frac{1}{16 \, y^{4}} + \frac{1}{2}\\ &=\left( y^2+ \frac{1}{4y^2}\right)^2. \end{align*}$$

   Então,

Função Comprimentod e arco

É útil termos uma função que meça o comprimento de arco de uma curva a partir de um ponto fixo inicial até outro ponto qualquer na curva. Deste modo, se a curva $C$ tem equação $y = f(x)$, $a\leq x\leq b$, seja $s(x)$ a distância ao longo de $C$ do ponto inicial $(a,f(a))$ ao ponto $(x,f(x))$. Então, $s$ é uma função, chamada função comprimento de arco, e é dada por

Exemplo

Encontre a função comprimento de $y = \ln(\cos(x))$ no intervalo $[0, \pi/3]$.

Solução: Se $y = \ln(\cos(x))$ então $y' = -\tan(x)$ e $\sqrt{1+(y')^2}= \sqrt{1+\tan^2(x)}=\sec(x)$. Logo

Neste exemplo, por que é importante que $x\in [0, \pi/3]$?

Exercício

Considere a função $f(x)=\ln(1-x^2),$ definida para $-1/2 \leq x\leq 1/2.$

1.Verifique que $\sqrt{1+f'(x)^{2}}$ é da forma $p(x)/q(x),$ em que $p(x)$ e $q(x)$ são polinômios de segundo grau.

2. Verifique que $\displaystyle \frac{p(x)}{q(x)}=A+\frac{B}{1-x^2},$ em que $A$ e $B$ são constantes.
3. Calcule o comprimento de arco da função $f(x).$

Superfícies de Revolução

Uma superfície de revolução é uma superfície gerada pela rotação de uma curva plana em torno de um eixo que se situa no mesmo plano da curva. Por exemplo, a superfície lateral de um cilindro circular reto pode ser gerada pela rotação de um segmento de reta em torno de um eixo paralelo a ele. Analogamente, a superfície de um tronco de cone pode ser gerada ao se fazer girar um segmento de reta em torno de um eixo contido no plano do segmento, como abaixo¹.

Vamos agora determinar uma forma de calcular a área de superfícies desse tipo. Denominaremos esse como o Problema da Área de Superfícies.

Problema da Área de Superfícies

Suponha que $f$ seja uma função lisa e não negativa em $[a, b]$ e que uma superfície de revolução seja gerada pela rotação da parte da curva $y =f(x)$ entre $x = a$ e $x = b$ em torno do eixo $x$ (como na imagem acima). Como podemos definir a área dessa superfície? Como podemos calculá-la?

A estratégia para estabelecer uma definição apropriada para área de uma superfície de revolução é similar à que usamos para definir integrais. Vamos decompor a superfície em pequenas seções cujas áreas possam ser aproximadas por objetos geométricos elementares, e, somando as aproximações das áreas dessas seções, obteremos uma soma de Riemann que aproxima a área desejada. Tomando o limite da soma de Riemann obteremos uma integral para o valor exato da área da superfície. Para implementar essa ideia, vamos dividir o intervalo $[a, b]$ em $n$ subintervalos, inserindo os pontos $x_1, x_2,\ldots, x_{n−1}$ entre $a = x_0$ e $b=x_n$. Assim como vimos na semana 10, os pontos correspondentes do gráfico de $f$ definem um caminho poligonal que aproxima a curva $y =f(x)$ acima do intervalo $[a,b]$. Quando esse caminho poligonal gira em torno do eixo $x$, gera uma superfície que consiste em $n$ partes, cada uma delas sendo um tronco de cone circular reto (ver figura abaixo).

Assim, a área de cada parte da superfície pode ser obtida a partir da a área da superfície de um tronco de cone com raios $r_1, r_2$ e comprimento lateral (geratriz) $l$, dada por

O $k$-ésimo tronco de cone terá raios $f(x_{k−1})$ e $f(x_k)$ e altura $\Delta x_k$. Seu comprimento lateral é dado por $L_k$, que é o comprimento do $k$-ésimo segmento de reta da poligonal que aproxima a curva. Como vimos na seção anterior, isso resulta em

Assim, a área lateral $S_k$ do $k$-ésimo tronco de cone será dada por

Somando todas essas áreas obtemos uma aproximação para a área da superfície $S$,

A próxima etapa é transformar essa expressão em uma soma de Riemman. Para isso vamos aplicar o Teorema do Valor Médio (Seção 2.2 das notas da semana 4). O teorema garante a existência de um ponto $x^*_k$ entre $x_{k-1}$ e $x_k$, tal que

Por outro lado, a continuidade de $f$ e o Teorema do Valor Intermediário (que foi estudado na disciplina Bases Matemáticas) garantem a existência de um ponto $x^{**}_k$ entre $x_{k−1}$ e $x_k$, de tal modo que

Substituindo esses dois resultados na expressão para a aproximação da área, segue

Embora esteja próxima, a última expressão não é exatamente uma soma de Riemann verdadeira, pois envolve duas grandezas distintas, $x^*_k$ e $x^{**}_k$, que fazem o papel de pontos amostrais. Entretanto, em cursos mais avançados pode-se provar que, devido à continuidade de $f$, isso não tem nenhum efeito sobre o limite. Desse modo, podemos supor que $x^{**}_k \to x^*_k$ ao tomar o limite. Com isso obtemos uma expressão para a área da superfície $S$,

A animação abaixo ilustra a "suavização" da superfície ao se aumentar a quantidade de subdivisões do intervalo $[a,x]$ e consequentemente a melhor aproximação com mais laterais de troncos de cone.

Definição

Se $f$ for uma função suave (multiplamente diferenciável) e não negativa em $[a, b]$, então a área da superfície de revolução gerada pela rotação da parte da curva $y=f(x)$ entre $x=a$ e $x=b$ em torno do eixo $x$ será definida por

$$S = \int_a^b 2\pi f(x)\sqrt{1+[f'(x)]^2}\,dx = \int_a^b 2\pi y\sqrt{1+\left(\frac{dy}{dx}\right)^2}\,dx. \nonumber \nonumber$$

Se $f(x)$ for invertível e diferenciável, então podemos obter $x$ como $x(y)$ e construir uma superfície de revolução em torno de $y$. Nesse caso a área da superfície pode ser expressa como

Note a semelhança, não por acaso, entre a expressão acima e a que foi obtida para o comprimento de arco de curvas.

Exemplo

Vamos determinar a área da superfície gerada pela rotação da parte da curva determinada por $f(x) = \sqrt x$ entre $x = 0$ e $x = \frac52$,

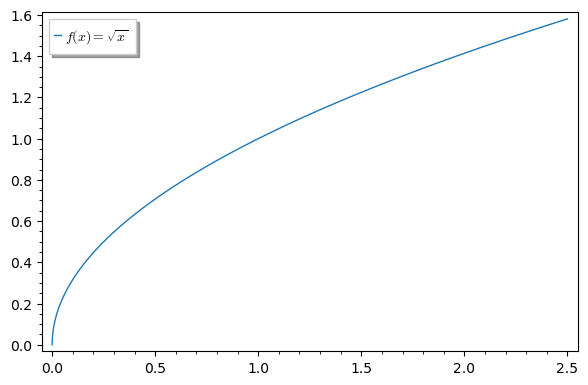
em torno do eixo $x$.

Para determinar a área da superfície de revolução precisamos calcular a integral

com $f(x)=\sqrt x$, e os limites de integração $a=0$ e $b = 2,5$. Sabemos que $f'(x) = \frac12x^{-\frac12}$, logo o integrando pode ser escrito como

Voltando à integral,

A superfície abaixo representa o sólido de revolução formado a partir de $f(x)$. A faixa laranja representa uma das laterais de tronco de cone utilizadas para construir a soma de Riemann, com $x_k=2$ e $x_{k-1}=1,98$.

Exercícios

1. Calcule a área das superfícies de revolução das funções abaixo.

   a. $f(x) = 5x,\quad$ $0\leq x \leq 1$;

   b. $f(x) = \sqrt{4-x^2},\quad$ $-1\leq x \leq 1$;

   c. $f(x) = \sin(x),\quad$ $0\leq x \leq 2\pi.\quad$ Veja a superfície nesse link.

2. Mostre que a área da superfície de uma esfera de raio $r$ é $4πr^2$ . Dica: Gire o semicírculo $y=\sqrt{r^2-x^2}$ em torno do eixo $x$ e escolha os limites de integração adequados.

3. Mostre que a área de superfície lateral de um cone circular reto de altura $h$ e raio de base $r$ é $\pi r\sqrt{r^2+h^2}$.

Volumes por Fatiamento

Veremos agora que a mesma estratégia de dividir regiões em intervalos pode ser usada para encontrar o volume de sólidos. A ideia é dividir o sólido em fatias finas, aproximar o volume de cada fatia, somar as aproximações para formar uma soma de Riemann e passar ao limite para produzir uma integral para o volume. O fato importante aqui é que as fatias finas devem ter seções transversais que não variam muito nem em tamanho nem em forma, isso nos permite calcular a área $A(x)$ dessas seções.

Conhecendo a área das seções transversais, seu volume será dado por

onde $\Delta x$ é a largura de cada partição. Podemos então estabelecer o seguinte problema.

Problema do Volume de Sólidos

Seja $M$ um sólido que se estende ao longo do eixo $x$ e que é limitado à esquerda e à direita, respectivamente, pelos planos perpendiculares ao eixo $x$ em $x = a$ e $x = b$. Queremos determinar o volume $V$ do sólido, supondo que sua seção transversal tenha área $A(x)$, conhecida em cada ponto $x$ do intervalo $[a, b]$.

Para resolver esse problema, dividimos o intervalo $[a, b]$ em $n$ subintervalos de espessura $\Delta x_k$, consequentemente o sólido também será dividido em $n$ fatias de espessura $\Delta x_k$. Somando essas aproximações, obtemos a seguinte soma de Riemann que aproxima o volume $V,$

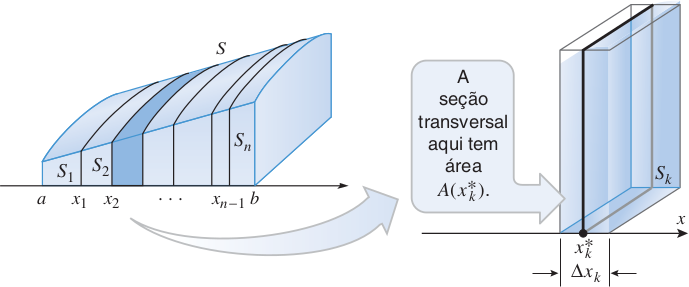
Tomando o limite quando $n$ cresce e as espessuras dos subintervalos tendem a zero, obtemos a integral definida

Em palavras, esse resultado afirma que o volume de um sólido pode ser obtido integrando-se a área da seção transversal de um extremo ao outro do sólido.

Exemplo

Encontre o volume de uma pirâmide com base quadrada de comprimento lateral de 10 u.m. (unidade de medida) e altura de 5 u.m.

Como cada seção transversal da pirâmide é um quadrado, para determinar sua área $A(x)$, precisamos apenas determinar os lados desses quadrados em termos da distância $x$ até o topo da pirâmide.

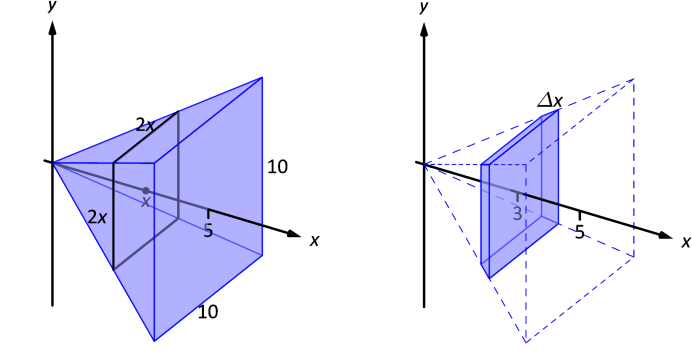
Para determinar os lados desses quadrados, podemos tomar uma seção transversal paralela ao eixo $y$ e que passa pelo eixo $x$. A interseção dessa seção com a superfície da pirâmide é descrita pelas retas $y=\pm x$ (se convença disso!). Logo, cada quadrado tem lado $2x$, e assim a área das seções transversais é $A(x) = 4x^2$. Com isso obtemos

Exercício

Use o método de volumes por fatiamento para mostrar que o volume de uma esfera de raio $r$ é $V=\frac43\pi r^3$.

Dica: Você pode fatiar a esfera como ilustrado nesse link., basta encontrar os raios dos discos.

Sólidos de Revolução

Um sólido de revolução é um sólido gerado pela rotação de uma região plana em torno de uma reta que está no mesmo plano da região. Podemos determinar volumes de sólidos de revolução combinando a técnica de fatiamento com o que vimos sobre superfícies de revolução. Para isso, observamos que a seção transversal do sólido, tomada perpendicularmente ao eixo $x$, no ponto $x$ é um disco de raio $f(x)$. A área dessa região é

Assim, o volume de sólido é então

Se, ao formar o sólido de revolução, considerarmos a área entre curvas, como vimos nas notas de aula da semana 8. Então, ao invés de um disco, a seção transversal será uma arruela, e região o volume será dado por

Exercício

Determine a área da superfície e o volume do solido de revolução gerado pela região entre as curvas $f(x) = \sqrt x+1$ e $g(x) = 1+\frac x2$. Para isso, primeiro determine onde essas curvas se intersectam, que coincide com os limites da região que gera o sólido. Você pode ver o objeto geométrico gerado pela revolução nesse link.

Dica: Para calcular a área da superfície de revolução você terá que integrar a função $\sqrt{\frac1x+4}$, cujo resultado é

$$\int \sqrt{\frac1x+4}\,dx=x\sqrt{\dfrac{1}{x}+4}+\dfrac{\ln\left(\sqrt{\frac{1}{x}+4}+2\right)}{4}-\dfrac{\ln\left(\left|\sqrt{\frac{1}{x}+4}-2\right|\right)}{4}+C.\nonumber$$

Para calcular essa integral você terá que combinar diferentes técnicas de integração vistas nas semanas 9 e 10.

Volume por Camadas Cilíndricas

O método para cálculo de volume que acabamos de discutir depende de nossa habilidade em computar a área da seção transversal de um sólido e integrá-la através dele. Nesta seção, vamos desenvolver outro método para encontrar volumes que pode ser aplicado quando não pudermos encontrar um expressão simples e geral para a área da seção transversão. A motivação vem do seguinte problema:

Volume de Sólidos II

Sejam $f$ contínua e não negativa em $[a, b]\; (0 ≤ a < b)$ e $R$ a região limitada acima por $y = f (x)$, abaixo pelo eixo $x$ e nas laterais pelas retas $x = a$ e $x = b$. Queremos determinar o volume $V$ do sólido de revolução $S$ gerado pela rotação da região $R$ em torno do eixo $y$.

Obs: O fato importante aqui não é a rotação em torno do eixo $y$, e sim que a curva $f(x)$ pode ser complicada o suficiente para que não possamos encontrar diretamente uma expressão para a área sob ela.

Uma camada cilíndrica é um sólido envolvido por dois cilindros retos concêntricos.

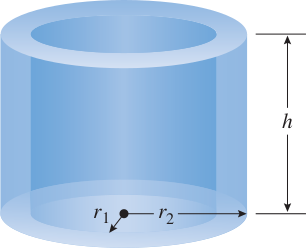
O volume $V$ de uma camada cilíndrica com raio interno $r_1$, raio externo $r_2$ e altura $h$ pode ser escrito como

onde $\frac12(r_2+r_1)$ é o raio médio da camada e $r_2-r_1$ sua espessura. A ideia agora é dividir o intervalo $[a, b]$ em $n$ subintervalos e, desse modo, subdividir a região $R$ em $n$ faixas, $R_1, R_2,\ldots, R_n$. Quando a região $R$ gira em torno do eixo $y,$ essas faixas geram os sólidos $S_1, S_2 ,\ldots, S_n$, alinhados um dentro do outro, e que podem ser aproximados por camadas cilíndricas.

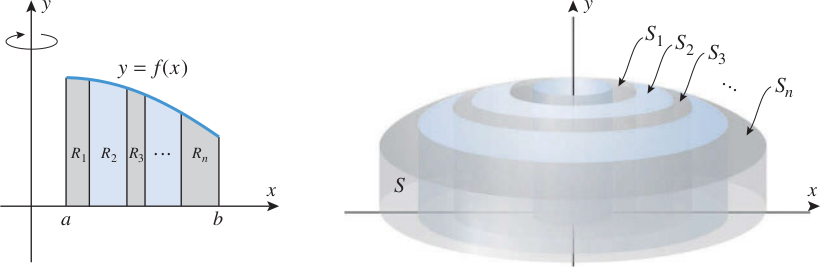
Assim, o volume $V$ do sólido pode ser aproximado somando os volumes das camadas. Isto é,

Para transformar esse volume em uma soma de Riemann, vamos supor que a $k$-ésima camada tenha raio interno $x_{k−1}$ e raio externo $x_k$. Logo sua espessura será dada por $\Delta x_k =x_k -x_{k-1}$. Se $x^*_k$ for o ponto médio do intervalo $[x_{k−1}, x_k ]$ e se construirmos um retângulo de altura $f(x^*_k)$ acima desse intervalo, então, fazendo esse retângulo girar em torno do eixo $y$, obtemos uma camada cilíndrica de altura $f(x^*_k)$, raio médio $x_k$ e espessura $\Delta x_k$. Usando a expressão que obtivemos para o volume de camadas cilíndricas, o volume da camada $V_k$ será dado por

Somando os volumes das $n$ camadas cilíndricas, obtemos finalmente soma de Riemann que aproxima o volume $V$

Tomando o limite quando $n \to \infty$ obtemos a integral definida

Exemplo

Vamos determinar a o volume do sólido delimitado por $f(x) = \cos x+2$, no intervalo entre $x=0$ e $x=2\pi$.

Usando a expressão para o volume acima, obtemos

Resolvemos essa integral usando o método de integração por partes (verifique!), que resulta em

O sólido é dado abaixo

Exercício

1. Use o método de camadas cilíndricas para encontrar o volume do sólido que resulta quando a região sombreada gira em torno do eixo indicado.

2. Use o método de camadas cilíndricas para encontrar o volume do sólido que resulta quando a região englobada pelas curvas gira em torno do eixo $y$.

​ a. $y=x^3, \quad x=1,\quad y=0.$

​ b. $y=1/x, \quad x=1,\quad x=3,\quad y=0.$

​ c. $y=\cos x^2, \quad x=0,\quad \frac12\sqrt \pi,\quad y=0.$

​ d. $y=\frac1{1+x^2}, \quad x=0, \quad x=1,\quad y=0.$

​ e. $y=2x-x^2,\quad y=0.$